LeetCode高频算法面试题 - 005 - 最长回文子串
漫步coding 5/2/2022
给你一个字符串 s,找到 s 中最长的回文子串。
题目难度: ★★★, 中等
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母组成
# 代码实现
tips: 以下代码是使用Go代码实现的不同解法, 文章最后可以看C++、C、Java、Python实现
1、动态规划
主要思路:
- 依次假设回文可能的长度是 2, 3, 4, len(str)
- 目前回文长度是sl
- 那么通过起点left, 可以判断终点的right = left + sl - 1
- 判断left 和 right 是否一致
- 如果left到right是回文字符串,判断是不是大于目前的回文长度, 如果是, 则使用更新到ml, si中.
func longestPalindrome(s string) string {
length := len(s)
if length < 2 {
return s
}
result := make([][]bool, length)
for i := 0; i < length; i++ {
result[i] = make([]bool, length)
}
ml, si := 1, 0
// 假设回文字串长度是 sl = right - left + 1
for sl := 2; sl <= length; sl++ {
// 左边界 i
for left := 0; left < length; left++ {
// 右边界 right - left + 1 = sl
right := left + sl - 1
if right >= length{
break
}
if s[left] != s[right] {
result[left][right] = false
} else {
if sl <= 3 {
result[left][right] = true
} else {
// result[left+1][right-1] 的长度是sl-2, 已经判断过了, 所以可以直接使用
result[left][right] = result[left+1][right-1]
}
}
if result[left][right] && sl > ml {
ml = sl
si = left
}
}
}
return s[si:si+ml]
}
执行结果分析:
时间复杂度:O(n^2) 其中 n 是字符串的长度。
空间复杂度:O(n^2)。

# 其他语言实现
1、Java
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 2) {
return s;
}
int strLen = s.length();
int maxStart = 0; //最长回文串的起点
int maxEnd = 0; //最长回文串的终点
int maxLen = 1; //最长回文串的长度
boolean[][] dp = new boolean[strLen][strLen];
for (int r = 1; r < strLen; r++) {
for (int l = 0; l < r; l++) {
if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
dp[l][r] = true;
if (r - l + 1 > maxLen) {
maxLen = r - l + 1;
maxStart = l;
maxEnd = r;
}
}
}
}
return s.substring(maxStart, maxEnd + 1);
}
}

2、Python3
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n < 2:
return s
max_len = 1
begin = 0
# dp[i][j] 表示 s[i..j] 是否是回文串
dp = [[False] * n for _ in range(n)]
for i in range(n):
dp[i][i] = True
# 递推开始
# 先枚举子串长度
for L in range(2, n + 1):
# 枚举左边界,左边界的上限设置可以宽松一些
for i in range(n):
# 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
j = L + i - 1
# 如果右边界越界,就可以退出当前循环
if j >= n:
break
if s[i] != s[j]:
dp[i][j] = False
else:
if j - i < 3:
dp[i][j] = True
else:
dp[i][j] = dp[i + 1][j - 1]
# 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if dp[i][j] and j - i + 1 > max_len:
max_len = j - i + 1
begin = i
return s[begin:begin + max_len]
Python好慢,花了7秒

3、C++
#include <iostream>
#include <string>
#include <vector>
using namespace std;
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
vector<vector<int>> dp(n, vector<int>(n));
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= n; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < n; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= n) {
break;
}
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};

# 几种语言运行效果对比
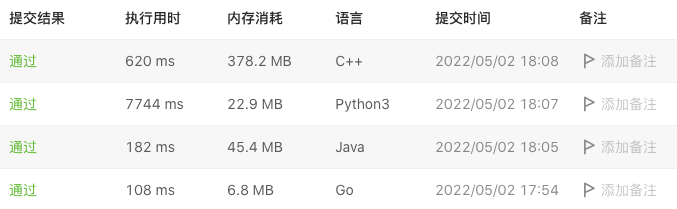
也欢迎关注我的公众号: 漫步coding。 一起交流, 在coding的世界里漫步。
