LeetCode高频算法面试题 - 011 - 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

题目难度: ★★, 中等

示例 1：

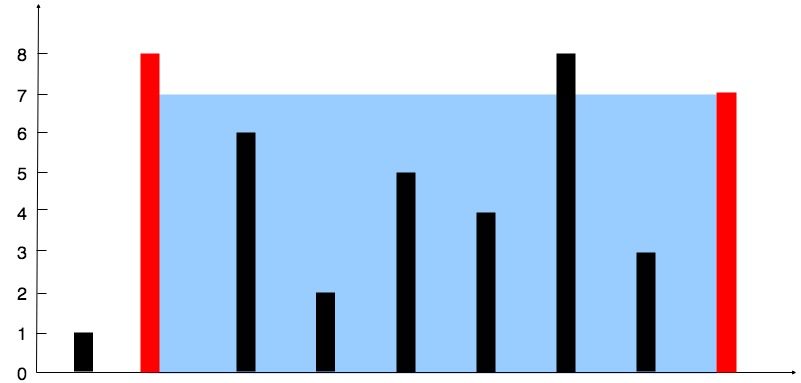
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

代码实现

设两指针 ii , jj ，指向的水槽板高度分别为 h[i] , h[j] ，此状态下水槽面积为 S(i, j)。由于可容纳水的高度由两板中的 短板 决定，因此可得如下 面积公式 ：

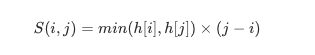
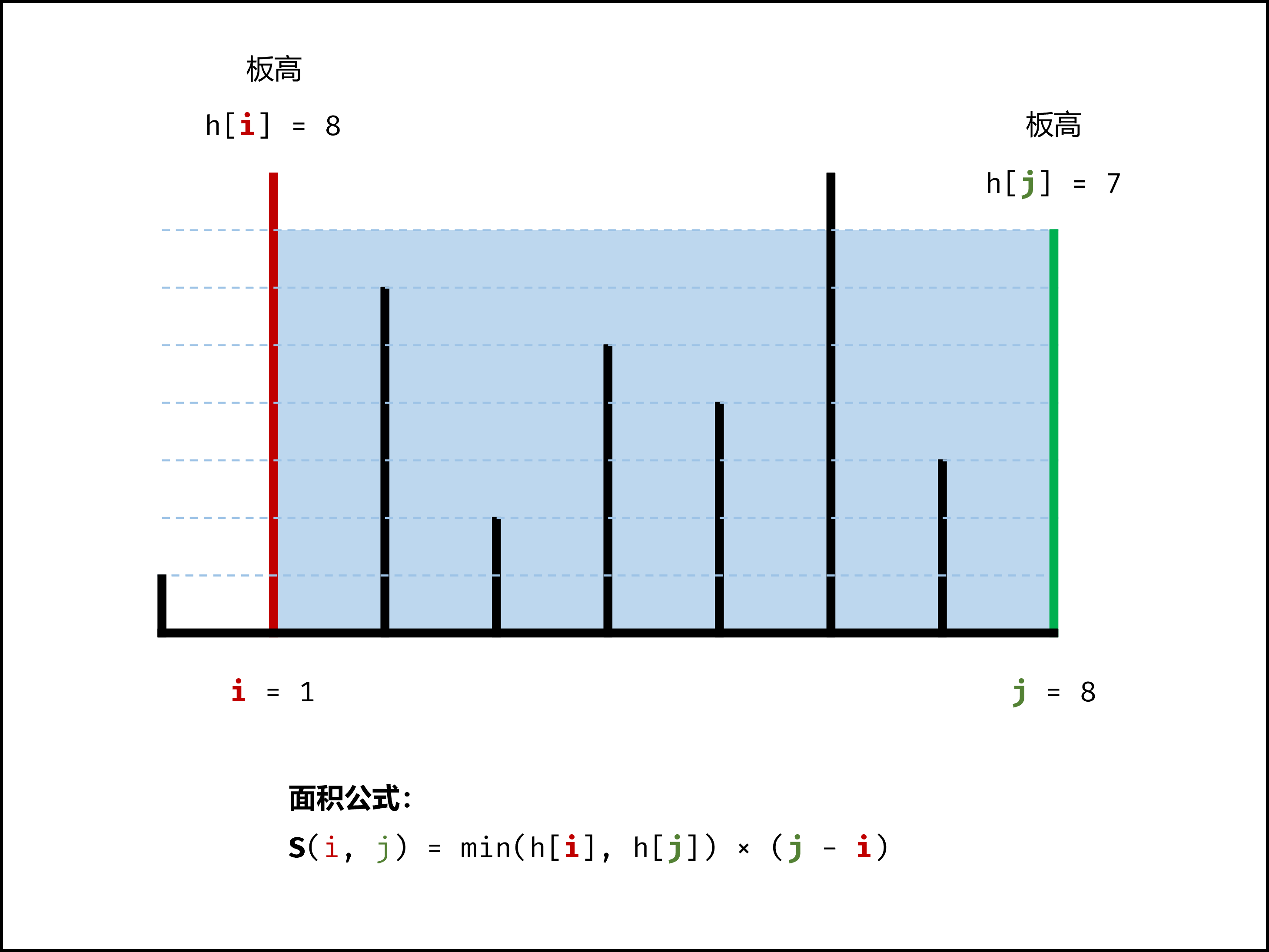
在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 -1−1​ 变短：

无论是移动短板或者长板，我们都只关注移动后的新短板会不会变长，而每次移动的木板都只有三种情况，比原短板短，比原短板长，与原短板相等；

如果向内移动长板，对于新的木板：

• 1.比原短板短，则新短板更短。
• 2.与原短板相等或者比原短板长，则新短板不变。
• 所以，向内移动长板，一定不能使新短板变长。
• 如果向内移动长板, 因此下个水槽的面积 一定变小

如果向内移动短板, 对于新的木板:

• 1.比原短板短，则新短板更短。
• 2.与原短板相等或者比原短板长，则新短板长。
• 所以，向内移动长板，可能使新短板变长。
• 如果向内移动短板, 因此下个水槽的面积 可能增大 。

tips: 以下代码是使用Go代码实现的不同解法, 文章最后可以看C++、C、Java、Python实现

具体代码如下:

func maxArea(height []int) int {
    i := 0
    j := len(height) - 1
    res := 0
    for {
        if i >= j{
            break
        }
        if height[i] < height[j]{
            if height[i]*(j-i) > res{
                res = height[i]*(j-i)
            }
            i += 1
        }else{
            if height[j]*(j-i) > res{
                res = height[j]*(j-i)
            }
            j -= 1
        }
    }
    return res
}

复杂度分析：

• 时间复杂度 O(N)： 双指针遍历一次底边宽度 N。
• 空间复杂度 O(1) ： 变量 i, j, res使用常数额外空间。

其他版本代码如下:

1、Python3

class Solution:
    def maxArea(self, height: List[int]) -> int:
        i, j, res = 0, len(height) - 1, 0
        while i < j:
            if height[i] < height[j]:
                res = max(res, height[i] * (j - i))
                i += 1
            else:
                res = max(res, height[j] * (j - i))
                j -= 1
        return res

2、Java

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                Math.max(res, (j - i) * height[i++]): 
                Math.max(res, (j - i) * height[j--]); 
        }
        return res;
    }
}

3、C++

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                max(res, (j - i) * height[i++]): 
                max(res, (j - i) * height[j--]); 
        }
        return res;
    }
};

几种语言运行效果对比

也欢迎关注我的公众号: 漫步coding。 一起交流, 在coding的世界里漫步。